Double Intercept Form

Here, we will discuss about the double intercept form of the equation of straight lines.

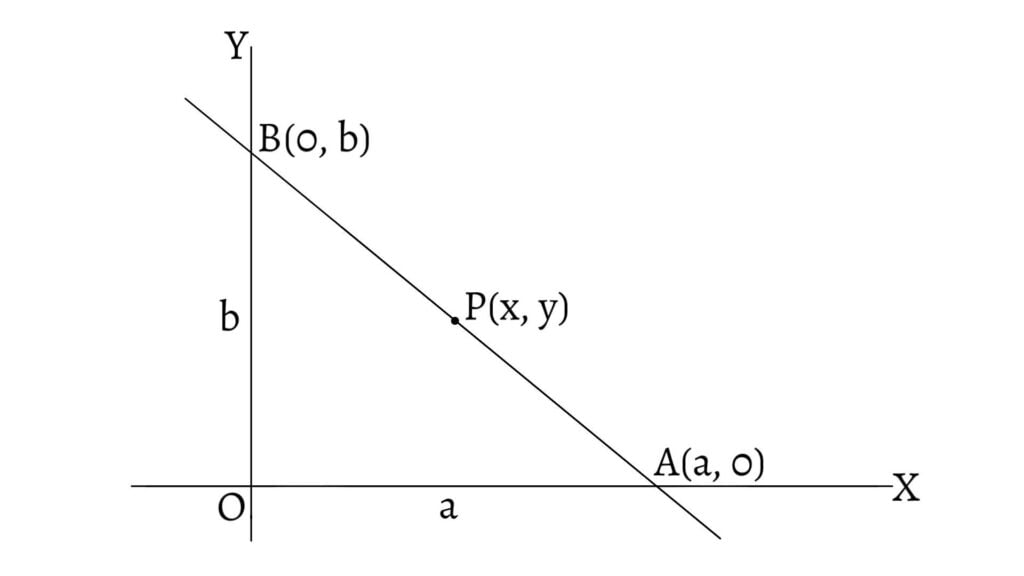
Let a straight line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively. Then, the intercepts on the x-axis and y-axis are $OA=a$ and $OB=b$ respectively. Also, let $P(x,y)$ be any point on $AB$.

Double Intercept Form" width="1024" height="576" />

This is the equation of the line whose intercepts are $a$ and $b$ and is known as the double intercept form. This form of the equation of a straight line cannot be used if the line passes through the origin or if it be parallel to any one of the axes.

Obtain the equation of the straight line passing through the point $(3,4)$ cutting off equal intercepts on the axes.

Since this line passes through the point $(3,4)$, \[3+4=a\] \[\therefore a=7\]

Putting the value of $a$ in $\text$, \[x+y=7\] which is the required equation of the line.

Find the equation of the straight line which passes through the point $(3,4)$ and makes intercepts on the axes, the sum of whose lengths is $14$.

Solving $\text$ and $\text$, \[3(14-a)+4a=a(14-a)\] \[42-3a+4a=14a-a^2\] \[a^2-13a+42=0\] \[(a-6)(a-7)=0\] \[\therefore a=6,7\]

Taking $a=6$, $b=14-6=8$. Then, the required equation of the line is \[\frac+\frac=1\] \[\therefore 4x+3y=24\]

Taking $a=7$, $b=14-7=7$. Then, the required equation of the line is, \[\frac+\frac=1\] \[\therefore x+y=7\]

Determine the equation of the line the portion of which, intercepted by the axes, is divided by the point $(-5,4)$ in the ratio $1:2$.

in the ratio 1:2" width="1024" height="576" />

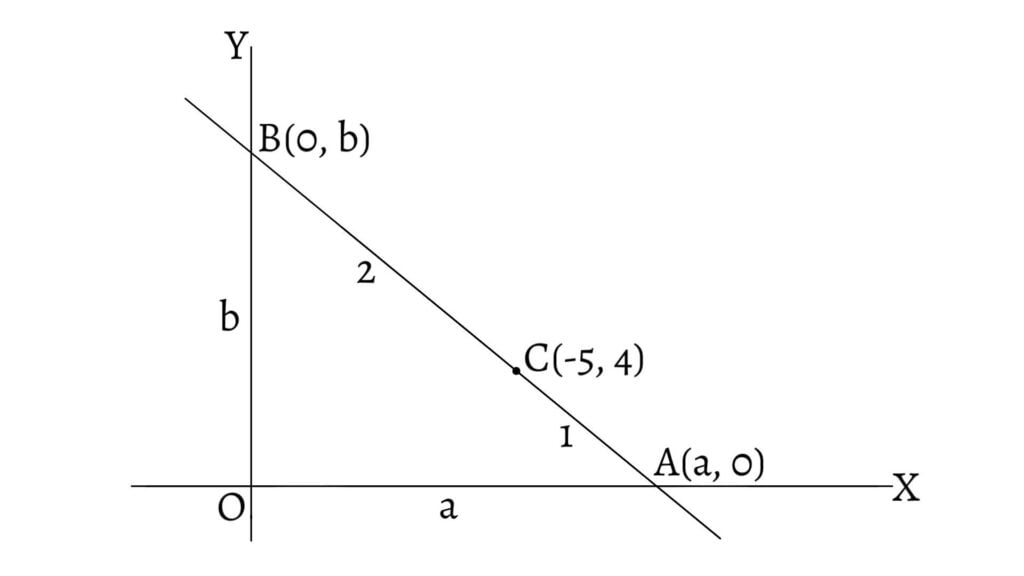
Let the line intersect x-axis and y-axis at $A(a,0)$ and $B(0,b)$ respectively and $AB$ is divided at $C$ in the ratio $1:2$. Then, from section formula for internal division, we have, \[-5=\frac\text< and >4=\frac\] \[-5=\frac\text< and >4=\frac\] \[\therefore a=\frac\text< and >b=12\]